Rotation Matrices
Linear Algebra
In physical situations, matrices arise when you want to work with and describe real world (multi-dimensional) objects. While there are other ways, using a matrix is often very convenient.
Let's say you're programming our manipulator amd you want to tell the robot that there is an obstacle five meters ahead, and two meters to the right. Now your robot then turns in place by 'Θ' degrees to the left. So, how do you calculate the location relative to the robot after the turn afterall we need to keep track of these obstacles.
If we were to describe the original coordinates of the obstacle with the a 2D matrix, that would be :
| X | 5 |
|---|---|
| Y | 2 |
This is where rotation matrices are powerful because of it's neatly written form especially with increasing dimentions such as our 3D world.
| X' |
| Y' |
| Cos(Θ) | -Sin(Θ) |
| Sin(Θ) | Cos(Θ) |
| 5 |
| 2 |
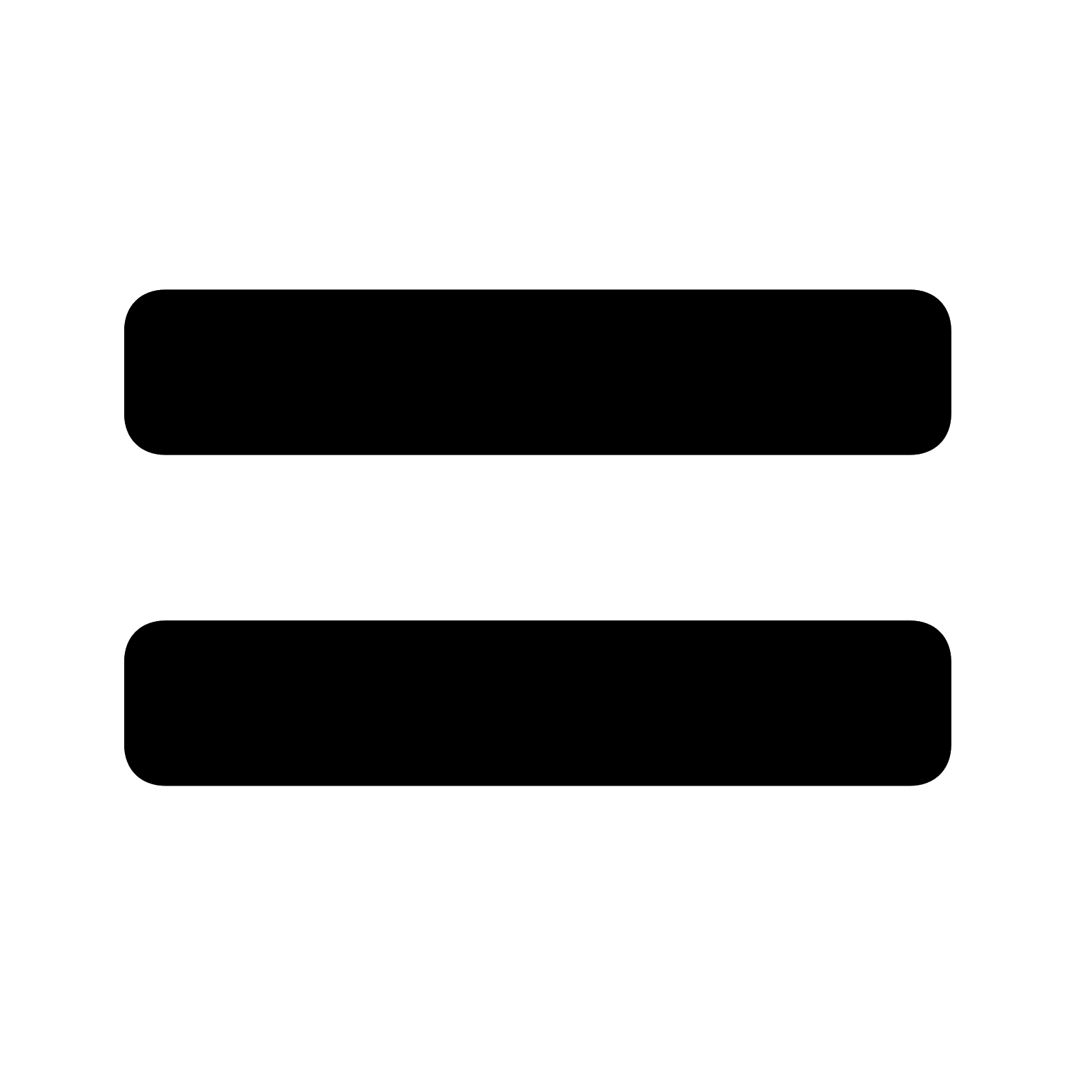
With X' and Y' being the coordinates of the obstacle according to the manipulator's reference.
This is a very simple example, but when we start writing out the equations that we will be later on using, you can see that as we scale dimensions and keep on rotating thus increasing the complexity of our operations, using matrices becomes more an more useful.
One of the most useful fact about matrices is the fact that if we keep on multiplying them as our operations gets more and more complex, we can simply use the very last product in order to determine the solution to the chain of operations. We will be talking more about this characteristic later as we move towards the Denavit-Hartenberg conventions.