Rotation Matrices
Representing Rotations
In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix.
| Cos(Θ) | -Sin(Θ) |
| Sin(Θ) | Cos(Θ) |
This matrix rotates points in the xy-plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv.
As previously seen, in the example:
| X' |
| Y' |
| Cos(Θ) | -Sin(Θ) |
| Sin(Θ) | Cos(Θ) |
| X |
| Y |
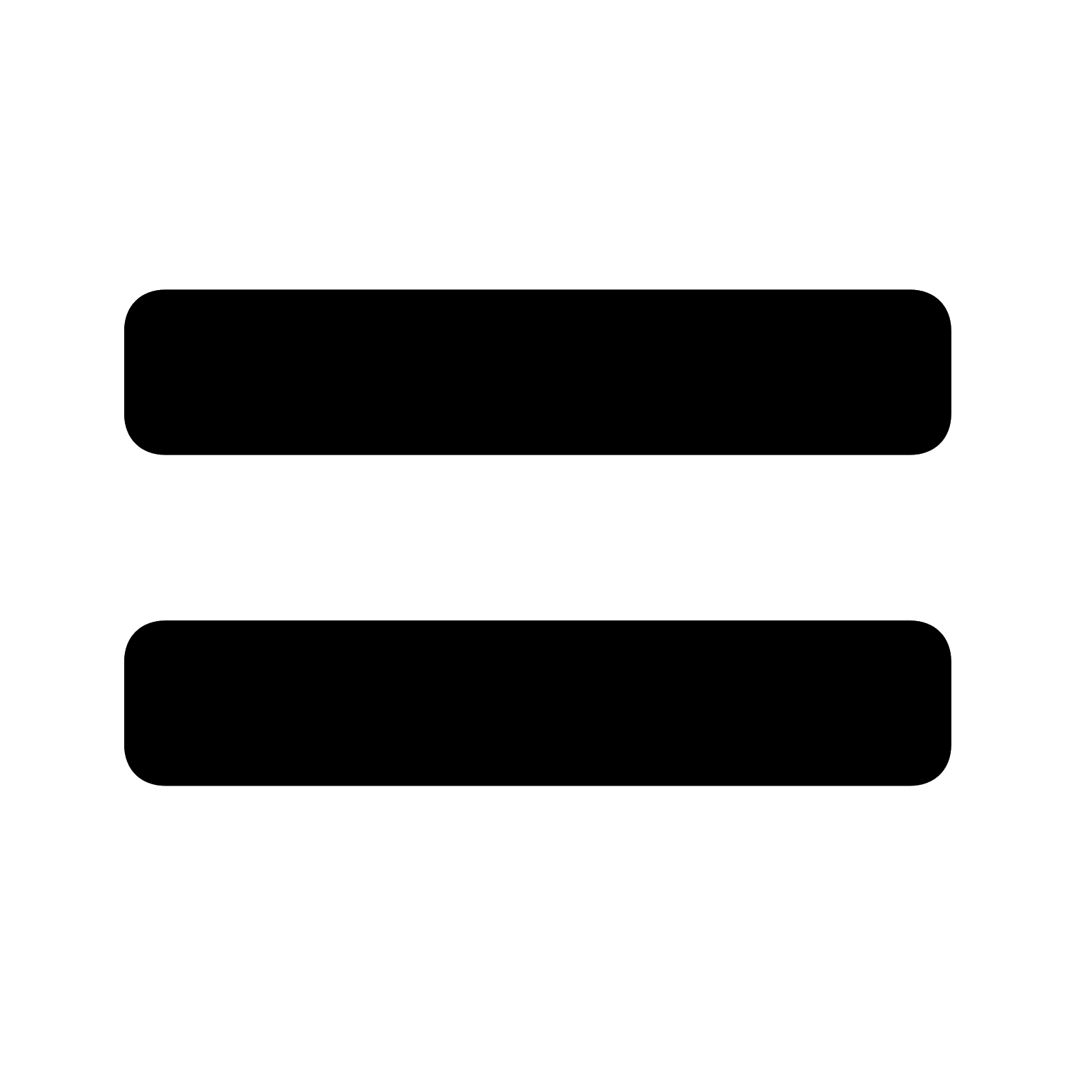
This operation the same as writing the following formulas :
A basic rotation (also called elemental rotation) is a rotation about one of the axes of a Coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x, y, or z axis, in three dimensions, using the right-hand-rule which codifies their alternating signs. It's very important for you to familiarize yourself with the right-hand-rule because these matrices can be taken as clockwise or counter-clockwise and it is important to have a commune convention when working with others.
The following example shows a rotation of θ = 90 done around the Z-axis.
As expected, a vector facing the X-axis, when rotated around the Z-axis by 90 degrees, is now facing the Y-axis.
When we are required to use multiple elementary rotations, we need to find a way to combine these rotations in a simpler format. Again using matrices for this purpose really simplifies things enormously.
For example, let's say we need to rotate a reference frame by the Y axis followed by the Z axis, as shown in the below picture.
In order to achieve this multiple rotation matrix, we simply need to figure out by how much we need to rotate each axis and simply multiple them.
Now we have a combination of elementary rotations which is in a very compact format. And all we need to do to go from reference frame A to B is to calculate B = R*A
Now it's your turn to practice! Please go to the next page in order to find some practice examples.